Materi kali ini mengenai salah satu cara yang sering dipakai dalam ilmu ukur (geometri) yakni kesebangunan dan kekongkureanan. Ikuti klarifikasi Mas Admin yang tanpa basa-basi dibawah ini.
A. KESEBANGUNAN
Dua buah berdiri datar dikatakan “sebangun” jikalau :
1. Sisi-sisi yang bersesuaian sebanding.
2. Sudut-sudut yang bersesuaian sebanding.
Sebanding artinya mempunyai perbandingan yang selalu sama. Sedang bersesuaian artinya yang mempunyai posisi yang sama.
Kesebangunan dilambangkan dengan tanda “ ”.
Contoh kesebanguanan dalam berdiri datar segitiga:
Gambar.1
Pada gambar.1, terlihat segitiga ABC sebangun dengan segitiga abc.
Kedua segitiga tersebut mempunyai panjang sisi-sisi yang bersesuaian sebanding, yakni :
AB : ab, BC : bc dan AC : ac
Kedua segitiga tersebut mempunyai besar sudut-sudut yang bersesuaian yang sebanding, yakni :
<A : <a, <B : <b dan <C : <c.
Kesebangunan sanggup diartikan bentuk sama tetapi ukuran beda. Karenanya dikatakan bukan sama tetapi sebanding.
B. KEKONGKRUENAN
Dua buah berdiri datar dikatakan “kongkruen” jikalau :
1. Sisi-sisi yang bersesuaian sama.
2. Sudut-sudut yang bersesuaian sama.
Kesebangunan dilambangkan dengan tanda “Ξ”.
Contoh kesebanguanan dalam berdiri datar segitiga:
Pada gamabr.2, terlihat segitiga ABC kongkruen dengan segitiga abc.
Kedua segitiga tersebut mempunyai panjang sisi-sisi yang bersesuaian sama, yakni :
AB=ab, BC=bc dan AC=ac
Kedua segitiga tersebut mempunyai besar sudut-sudut yang bersesuaian yang sama, yakni :
<A = <a, <B= <b dan <C = <c.
Kongkruen sanggup diartikan sama dan sebangun. Seperti copyan dari bentuk sebelumnya, segitiga abc cioyan dari segitiga ABC.
C. BENTUK KESEBANGUNAN DAN KEKONGKRUENAN
Gambar.3
Panjang EF = (a x d) + (b x c)
c + d
Panjang AB = ( ((EF) – a) x d ) + EF
c
Panjang CD = EF – ( (d – EF) x c )
d
C2. Bentuk Kedua
Panjang EF = AB - CD
2
Panjang CD = AB – 2 EF
Panjang AB = CD + 2 EF
C3. Bentuk Ketiga
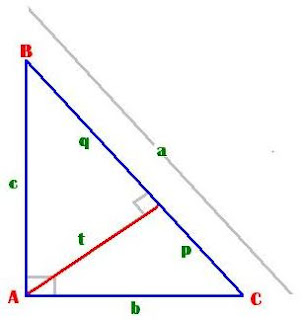
Gambar.5
Panjang b2 = ap
c2 = aq
t2 = pq ATAU t2 = bc/q
C4. Bentuk Keempat
Gambar.6
Materi yang sering keluar dalam Ujian Nasional yaitu :
1. Menentukan garis atau sudut mana yang sama dalam suatu bidang datar, contohnya dalam berdiri segitiga.
2. Menghitung panjang suatu garis pada kesebangunan/Kekongruenan bentuk 1 hingga 4.
SOAL LATIHAN :
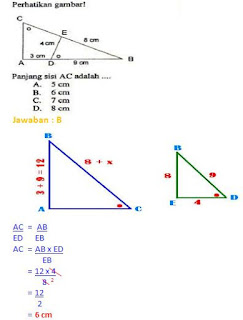
1. UN 2009
Mudah-mudahan klarifikasi singkat ini berguna, terutama bagi adik-adik yang masih duduk dibangku Sekolah Menengah Pertama. Teruslah berlatih mengerjakan soal-soal yang ada. Karena semakin banyak berlatih maka pemahaman bahan makin terasah.
Mas Admin menggunakan sandard soal-soal UN, alasannya menyerupai kita maklumi tujuan UN yaitu menilai hingga dimana standard yang telah ditetapkan negara sanggup dicapai. Artinya tolak ukurnya yaitu nasional, bukan lagi tingakt terkecil yakni tingkat sekolah. Semakin tinggi nilai UN yang dicapai suatu sekolah maka sekolah tersebut telah mencapai target yang ditentukan negara,
Demikian ulasan yang sanggup aku berikan. Sampai ketemu di lain materi, tetap semangat!
Salam,
Mas Admin
Mas Admin
















0 Response to "Matematika Smp : Kesebangunan Dan Kekongkruenan"